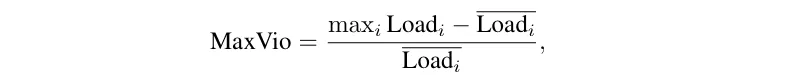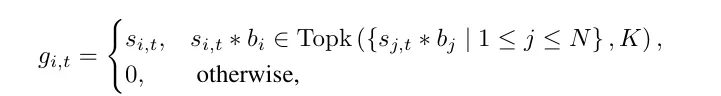DeepSeek如何打破MoE中隐藏的瓶颈? 辅助无损负载均衡策略
这篇文章探讨了 DeepSeek 模型中与专家混合 (MoE) 相关的另一个关键架构突破:辅助无损负载均衡策略。在本文中,我们将深入探讨 DeepSeek 如何解决 MoE 的隐藏瓶颈——负载均衡——同时消除梯度干扰并保留因果关系,为基于专家的模型的效率设定新标准。
背景¶
首先介绍专家混合 (Mixture-of-Experts,MoE) 的基础知识,解释为什么负载平衡很重要,并回顾以前的工作,包括辅助损失方法(auxiliary loss methods)和专家选择(Expert Choice)。
Transformers中的MoE¶
MoE 代表 Mixture-of-Experts,在 Transformer 模型的上下文中,这通常是指将每几个 Transformer 层中的 FFN 替换为多个 FFNs,每个 FFN 都充当专家。因此,当输入Token出现时,门控作将选择 top-K 专家,并仅将输入Token路由到选定的 FFN,以便仅激活选定的专家。
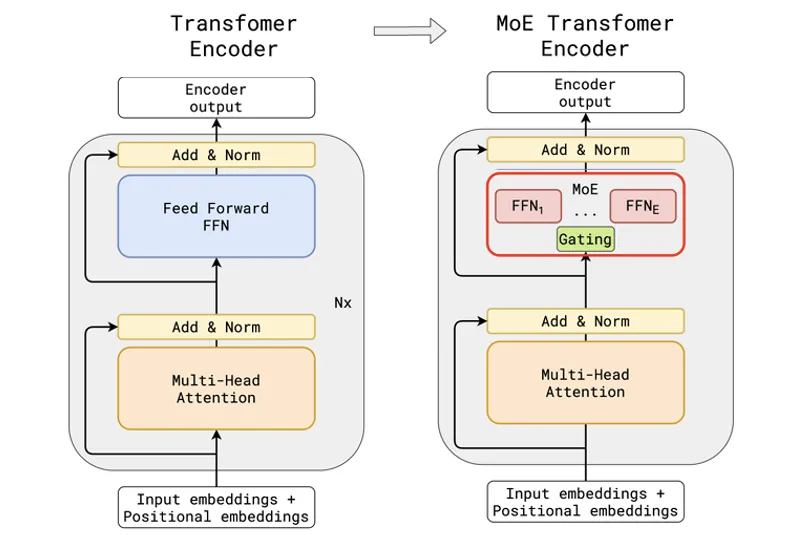
如下图所示,其中左侧标准 Transformer 层中的 FFN 子层被 MoE 层取代。
在我们之前的餐厅类比的例子中,我们解释了 MoE 的概念,一家提供多种美食的餐厅,其中每位厨师担任专家,主厨担任门控作,将每道菜分配给具有适当技能的特定厨师。
为了确保这样的系统有效运行,我们需要:
-
每个专业厨师都必须掌握自己菜肴所需的技能(例如,包饺子的厨师必须知道如何制作饺子),同时他们可以集体处理所有菜肴。
-
主厨对所有专业厨师的专业知识都有很好的了解,可以有效地分配订单。
在 MoE 中,前者对应于专家专业化与知识共享之间的权衡,我们在 DeepSeekMoE 中对此进行了详细讨论。后者反映了负载均衡的重要性,这是本文的主要主题。
那么,是什么让负载平衡如此重要呢?
原因是当负载不平衡发生时,MoE 无法正常运行,最常见的问题称为路由崩溃(route collapse),即只有一小部分专家收到大部分 输入token,而其他专家没有得到充分利用。
因此,大多数计算都是由超负荷的专家进行的,这会导致硬件利用率出现瓶颈,因为专家通常分布在多个 GPU 核上。
由于梯度冲突,路线崩溃也会导致训练不稳定。由于超载的专家会收到更多的 input token,他们也会积累更大的梯度,并且比低负载的专家学习得更快。因此,来自超负荷专家和低负荷专家的梯度可能在幅度和方向上都有所不同,从而使训练过程更难收敛。
最后,MoE 中的负载不平衡也会导致性能不佳和泛化能力差,因为负载不足的专家没有获得足够的训练token来学习有意义的知识。
由于负载均衡在 MoE 中非常重要,因此已经提出了不同的技术来处理这个问题。在前面的这些工作中,最常用的策略是为为负载均衡添加辅助损失(adding auxiliary loss for load -balancing)和专家选择(Expert Choice)。
具有辅助损失的负载均衡¶
改进负载均衡的一种常见策略是在模型训练中的原始目标之上引入辅助损失函数。
上图显示了辅助损失函数的示例,其中
-
N 是专家数,T 是 Token 数量,K 是每个输入 Token 的已激活专家数。
-
$ s_{i, t} $ 是 Gating 的输出,已通过 Softmax 标准化为 [0, 1],表示第 t 个token选择第 i 个专家的概率。向量 $ u_t $ 是第 t 个标记的输入隐藏状态,而 $ e_i $ 是第i个专家的质心,可以看作是过去路由到第 i 个token的平均token embedding。因此,$ s_{i, t} $ 衡量当前输入与第 i 个专家接收的平均令牌的接近程度。
-
因此,$ P_i $ 可以看作是在整个输入序列中选择第 i 个专家的平均概率。
-
$ f_i $ 表示路由到第 i 个专家的token的比例。
请注意,$ f_i $ 是不可微分的,因此最小化上述损失函数实际上变成了最小化 $ s_{i,t}$ 。此外,由于 $ f_i $ 取决于 $ s_{i, t} $,因此对 $ s_{i, t} $ 应用的调整也会影响 $ f_i $,因此分配给每个专家的载荷将被调整。
然而,用这种辅助损失来平衡负载是有代价的,因为它的梯度可能会干扰语言建模目标的梯度,导致模型性能不佳,尤其是在过载的专家的$ f_i和P_i $ 都变得非常大的极不平衡的情况下。
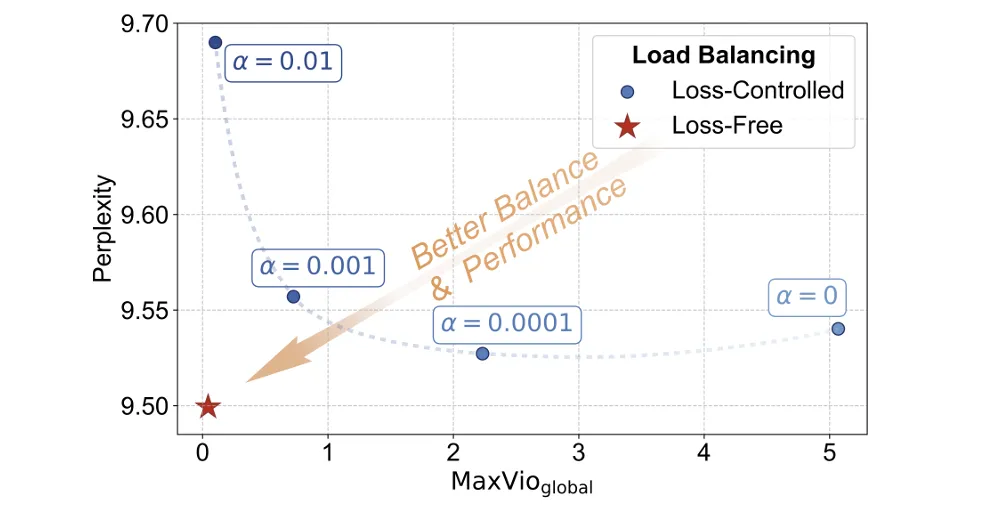
因此,用这种方法平衡负载需要仔细权衡辅助损失。为了更清楚地看到这一点,辅助无损负载均衡策略的作者通过训练具有不同 alpha 值的模型进行了一项实验,结果如下图所示,其中 y 轴表示模型性能的困惑度(perplexity),x 轴显示 MaxVio,这是一个表示负载不平衡程度的指标,其中更高的 MaxVio 意味着更严重的负载不平衡(i 代表第 i 个专家):
如上图所示,当 alpha 太小 (alpha = 0) 时,MaxVio 保持高水平,这意味着辅助损失不够有效,无法实现负载均衡目标。另一方面,当 alpha 变得太大 (alpha = 0.01) 时,模型最终会产生更高的困惑度。
总之,辅助损失控制负载平衡是一把双刃剑,如果不仔细调整 alpha,可能会对模型性能产生负面影响。在实践中,由于资源限制,在 LLM 训练期间调整 alpha 具有挑战性,这进一步使优化过程复杂化。
上图还将所提出的无损方法放在同一个 Perplexity-MaxVio 图表下,它同时实现了低 perplexity 和低 MaxVio,显示了 loss-free 方法的有效性。
我们在这里要提到的另一项先前的工作是 Expert Choice,它通过将路由策略从 “token choice” 转变为 “expert choice”,提出了一种简单而有效的负载均衡方法。
更具体地说,MoE 路由中的门控分数通常是在亲和矩阵之上使用 Softmax 计算的,如图 2 所示。传统的路由方法从 token 维度应用 Softmax 为每个 token 选择专家,因此这些方法被称为 “token choice”。问题是,在这样的机制下,我们无法控制每个专家将收到多少 Token,这最终会导致负载不平衡问题。
另一方面,专家选择,通过选择路由到每个专家的token,从专家维度应用 Softmax。因此,每个专家接收的token在设计上是完美平衡的,因此不需要辅助损失来进行负载均衡。在原始论文 Expert Choice中,这种方法展示了更好的模型性能和更快的训练速度。
然而,Expert Choice 的一个限制是未来的token泄漏问题(future token leakage issue),因为每个专家在看到所有token路由分数后决定处理哪个token,这违反了因果关系,在文本生成和机器翻译等自回归任务中可能是一个严重的问题。
DeepSeek 的辅助无损负载均衡¶
为了在不引入梯度推理的情况下解决负载均衡问题,DeepSeek 提出了一种称为无损平衡(Loss-Free Balancing)的新技术,通过直接调整门控分数 $ s_{i,t} $。
正如我们之前提到的,当我们最小化图 2 中所示的辅助损失(auxiliary loss)时,最终通过调整 $ s_{i, t} $ 来最小化 $ P_i $。
因此,如果我们可以直接调整 $ s_{i, t} $,理论上我们应该能够达到与应用辅助损失(auxiliary loss)类似的效果。
为此,将专家级偏差添加到每个专家的门控分数中,如下图所示。请注意,b_i 不**用于最终的门控分数(正如我们稍后将看到的,这种偏差也是不可微分的),但它在 TopK 中用于选择专家:
上述偏差 $ b_i $ 的计算方式非常直观,如下图所示:我们首先得到分配给每个专家的平均 Token 数量和他们的平均值,然后得到每个专家分配的 Token 与平均值的差值,偏差是由这个差值(或误差)的符号乘以固定的更新率**来确定的, 这是一个可优化的超参数。在后面的章节中,我们将看到更多关于这个超参数影响的实验。
现在,我们可以在下表中总结不同负载均衡方法的优势和局限性:
我们在图 3 中看到,所提出的方法在模型性能和负载均衡方面实现了更好的权衡,但仍有许多方面需要检查。在下一节中,我们将仔细研究实验结果。
评估¶
基本上,有三个重要问题需要回答:
-
所提出的方法能否在性能和负载均衡之间实现更好的权衡?
-
图 5 中的更新率 u 有什么影响?
-
我们能否进一步优化偏差更新规则(鉴于它如此简单)?
性能与负载均衡¶
为了回答第一个问题,作者在 1B 和 3B 模型上进行了实验,以比较损失控制(loss-controlled)和无损负载均衡(loss-free load balancing)的 Perplexity 和 MaxVio,结果如下图所示:
上面的结果类似于我们在图 3 中看到的结果,所提出的方法同时实现了较低的 Perplexity 和较低的 MaxVio。
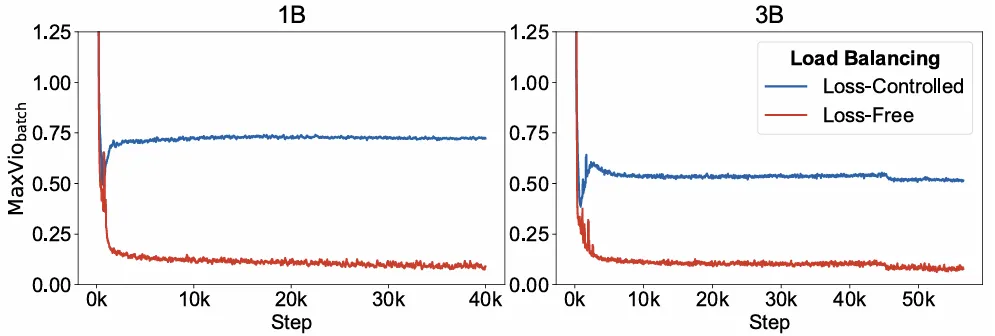
除了评估最终的检查点外,作者还展示了训练过程中的 MaxVio 曲线,以便我们可以更好地了解所提出的方法在整个训练过程中的表现,如下图所示:
如上图所示,在 1B 和 3B 设置中,无损方法在训练过程中都表现出更好的负载均衡能力,显示了该方法的稳定性。
超参数 (Update Rate) 的影响¶
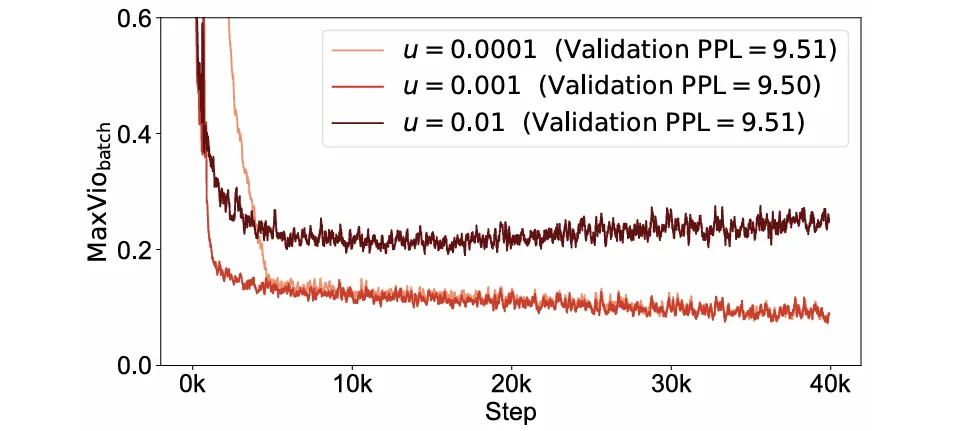
如图 5 所示,所提出的方法引入了一个新的超参数 u,称为更新率,因此一个自然而然的问题是这个超参数将如何影响无损方法的有效性。更具体地说,我们需要了解无损方法对 u 的值是敏感还是稳健,以及如何选择一个值以最好地利用所提出的方法。
如前所述,在门控分数中添加偏差项在概念上类似于对门控分数应用直接梯度更新,而不依赖于通过损失函数的反向传播。在这种情况下,更新速率 u 与梯度更新中的步长具有类似的作用。从这个角度来看,我们可以预期类似的影响:较小的更新速率可能会导致收敛缓慢,而过大的更新速率可能会导致不稳定和波动。
在原始论文中,作者以 1e-4 到 1e-2 的不同更新速率进行了实验,结果如下图所示:
正如我们所预期的那样,当您太小时(在本例中为 1e-4),MaxVio 下降速度会变慢,但过大的 u 也会产生负面影响,由于波动较大,导致整个训练过程中的 MaxVio 更高。
其它偏差更新规则¶
为了回答第三个问题,作者尝试了几种替代策略,并将它们与建议的版本进行了比较:
-
变体 1:使用 $ e_i $ 的值计算偏差,而不仅仅是其符号,即从 $ b_i = b_i +u∗sign**(e_i)$ 到 $ b_i = b_i +u∗e_i $。
-
变体 2:使用乘法偏差而不是加法偏差。
其中变体 2 可以更正式地描述如下:
正如他们的实验所示,变体 1 会导致负载均衡略好,但并没有提高模型性能:
变体 2 甚至显示出略差的模型性能:
以上所有结果表明,最简单的策略被证明是最好的。
总结¶
在本文中,我们解释了 DeepSeekMoE 中使用的辅助无损负载均衡方法,这是 DeepSeek 模型中采用的主要架构创新之一。
更具体地说,我们首先介绍了 Mixture-of-Expert (MoE) 的基本原理,强调了负载均衡的重要性,并回顾了以前的解决方案,包括辅助损失方法和 Expert Choice。然后,我们解释了 DeepSeek 的无损负载均衡方法及其性能。
(文章译自deepseek-v3-explained-3-auxiliary-loss-free-load-balancing)