DeepSeek-R1和FP8混合精度训练以及FP8量化实现

• DeepSeek-R1 和 FP8 混合精度训练(译)
  • 为什么我们要关注 FP8 训练？
  • 在 FP8 中工作有几个权衡
  • DeepSeek 的解决方案
• 不同框架对DeepSeek-V3_FP8量化支持
• SGLang框架deepseek FP8分块量化支持
• 高性能Cutlass实现：Blockwise Scaling和Groupwise Scaling
  • 分块缩放实现
  • 分组缩放实现

DeepSeek-R1 和 FP8 混合精度训练(译)

(本小节译自deepseek-r1-and-fp8-mixed-precision-training)

深度探索（DeepSeek）发布了其推理模型深度探索-R1（DeepSeek-R1），震惊了世界。与 OpenAI 的 o1 和Google Gemini的Flash Thinking类似，R1 模型旨在通过在响应提示之前生成一条“思维链”来提高回复质量。R1 引起的兴奋源于它在包括数学、编码以及英语和中文语言理解等几个行业标准基准测试中与 o1 达到同等水平，同时它也是开源的，并且可以通过深度探索 API 以极低的成本获得。

DeepSeek 的技术报告涵盖了广泛的性能优化技术，这些技术使其在高效的大型语言模型训练和推理方面取得了突破性成果。其中许多技术已被用于训练 DeepSeek-V3，这是一个与 Anthropic 的 Claude Sonnet 和 OpenAI 的 GPT-4o 相当的模型，R1 模型是通过微调（fine-tuning）和强化学习从 DeepSeek-V3 中获得的。在这篇文章中，我们将特别关注 DeepSeek 的基础 DeepSeek-V3 模型的 FP8 混合精度训练策略（在 DeepSeek-V3 论文的 3.3 节和下图（该论文的图 6）中进行了描述）。

和往常一样，一个核心瓶颈是矩阵乘法（也称为“matmul”或“GEMM”），如图表中的黄色方框所示。如图所示，模型权重存储在 FP8 中，所有矩阵乘法都在 FP8 中进行，并带有 FP32 累加。激活值和梯度存储在 BF16 中，FP32 也用于一些内部计算。

DeepSeek-V3 论文中的图 6，展示了其线性层中使用的各种浮点精度。

为什么我们要关注 FP8 训练？

在 NVIDIA 显卡上，通用矩阵乘法（GEMM）计算可以利用显卡的 Tensor Core 提供的硬件加速。在 Hopper 架构上，FP8 GEMM 得到原生支持，并实现了可能的最高计算吞吐量，在 H100 SXM 显卡上宣称约为 2 petaFLOPS。实际上，NVIDIA 认为低精度计算非常重要，以至于它正在通过 Blackwell 将 Tensor Core 的功能扩展到 FP4 和 FP6。以低精度存储模型权重还可以减少模型的总体大小，减轻对内存和显卡间通信通道的压力，而这些通道已经被推向极限以跟上 Tensor Core 的步伐。

在 FP8 中工作有几个权衡

首先，为了防止溢出，通常在将更高精度的权重或激活矩阵量化之前，将其缩放到 FP8 可表示的范围——例如，通过将整个张量除以其最大元素。该最大元素被单独保留，并在与量化张量的每次矩阵乘法中用作缩放因子。然而，这使得量化过程对异常值极为敏感：在某些层中存在非常大的权重可能会迫使所有其他权重被量化为 0。DeepSeek 团队通过引入分块和分片缩放( blockwise and tilewise scaling)来处理这个问题，其中权重矩阵的每个 128×128 子矩阵，以及激活向量的每个 1×128 子向量，分别进行缩放和量化。然后，由于在 GEMM 的“内部”或“收缩”维度上存在不同的缩放因子，重新缩放计算需要融合到矩阵乘法主循环中。这要求团队编写一个自定义的带re-scaling的 FP8-GEMM 内核。我们还注意到，由于训练不稳定，仅分块量化（即对于激活也是如此）被证明对于他们的目的是不够的；参见论文附录 B.2 中描述的消融研究。

此外，在 Hopper GPU 上的最佳通用矩阵乘法（GEMM）使用了线程束组范围的矩阵乘累加指令（warpgroup-wide MMA instructions，WGMMA），在 GEMM 教程中作为一部分对其进行了详细描述。在这些指令下，Hopper GPU 流式多处理器（SM）上的所有张量核心协同计算矩阵乘积的片段。然而，这就引出了 FP8 的第二个问题。DeepSeek 研究人员发现，FP8 张量核心使用了一种特定的“定点累加”策略，实际上只使用了 14 位精度，而不是真正的 FP32 精度；参见论文的 3.5.2 节。这导致了训练不准确性随着模型尺寸的增大而增加。

DeepSeek 的解决方案

DeepSeek 的解决方案是将部分累加操作移到 Tensor Core 之外。他们的通用矩阵乘法（GEMM）内核在 Tensor Core 内部执行每一系列连续的 4 次WGMMA操作，并以较低精度格式进行累加，但随后将结果添加到一个单独的基于寄存器的累加器张量中，该张量为单精度浮点数（FP32）格式。第二次加法是使用 CUDA Core（GPU 用于非矩阵乘法的 FP32 算术的标准执行单元）执行的，因此以普通的 FP32 精度进行，从而减轻了精度损失。反量化比例因子也应用于这个 FP32 累加器。

论文中的图 7(b)：在 DeepSeek-V3 的训练过程中使用的混合精度矩阵乘法技术，其中在Tensor Cores上进行的低精度 WGMMA 操作与在 CUDA Cores上进行的高精度累加交替进行。

论文作者引用了 NVIDIA 的CUTLASS 库来介绍这项技术。自 3.2 版本以来，CUTLASS 就支持了将 FP8 矩阵乘法提升为在 CUDA 核心中进行 FP32 累加。此外，分块缩放是在这个 PR中添加的，并在 3.7 版本中合并到主分支，并且由于这个 PR（为了清晰起见，将这个概念重命名为分组缩放），很快将支持分块缩放。作为 CUTLASS 用户，你可以通过将KernelScheduleType设置为KernelTmaWarpSpecializedCooperativeFP8BlockScaledAccum，使用CollectiveBuilder来调用具有提升的 FP32 累加和分块缩放的 Hopper FP8 GEMM（参见示例 67）。实际上，CUTLASS 的 Hopper FP8 GEMM 内核默认使用 CUDA 核心累加技术。或者，仅支持在Tensor Cores中, 你可以使用诸如KernelTmaWarpSpecializedFP8FastAccum的调度进行累加；这是以较低的准确性换取更好的性能，这对于推理应用可能效果更好。

不同框架对DeepSeek-V3_FP8量化支持

SGLang框架deepseek FP8分块量化支持

SGLang框架对deepseek v3模型FP8分块量化支持。

Description: SGLang implements block-wise FP8 quantization with two key optimizations:

Activation: E4M3 format using per-token-per-128-channel sub-vector scales with online casting.

Weight: Per-128x128-block quantization for better numerical stability.

源码实现：fp8_kernel.py

高性能Cutlass实现：Blockwise Scaling和Groupwise Scaling

当我们采用更窄的数据类型时，传统的缩放方法难以保持准确性，特别是对于 8 位浮点类型（例如，e5m2_t，e4m3_t）。典型的通用矩阵乘法（GEMM）操作使用张量缩放，公式为D = alpha * (A @ B) + beta * C，但更窄的数据类型需要更精细的缩放技术。此拉取请求（PR）添加了分块缩放策略，以提高准确性，同时努力不损失性能。

CUTLASS支持的四种缩放模式，不同模式的量化粒度不一样：

• 张量级缩放（Tensorwise Scaling）： 每个张量使用单个缩放因子，在尾声（epilogue）中应用。

• 行级缩放（Rowwise Scaling）： 使用一个行向量进行缩放，对于操作数 A 的维度为 Mx1，对于操作数 B 的维度为 1xN，避免沿归约维度进行缩放。这也可以在尾声中使用 EpilogueVisitorTree 来处理。

• 分块缩放（Blockwise Scaling）： 引入一个 2D 缩放张量，每个 CTA 块分配一个缩放值。由于此缩放涉及归约维度 (M, N, K)，因此必须在主循环中应用，这会影响性能。为 CUTLASS F8 GEMM 实现的分块缩放，通过共享内存暂存缩放张量，对分组缩放的支持做了准备。

• 分组缩放（Groupwise Scaling）： 使用一个 2D 缩放张量，每个 CTA 块有多个缩放值。缩放粒度独立于 CTA 块配置，为将来的实现提供了更大的灵活性。

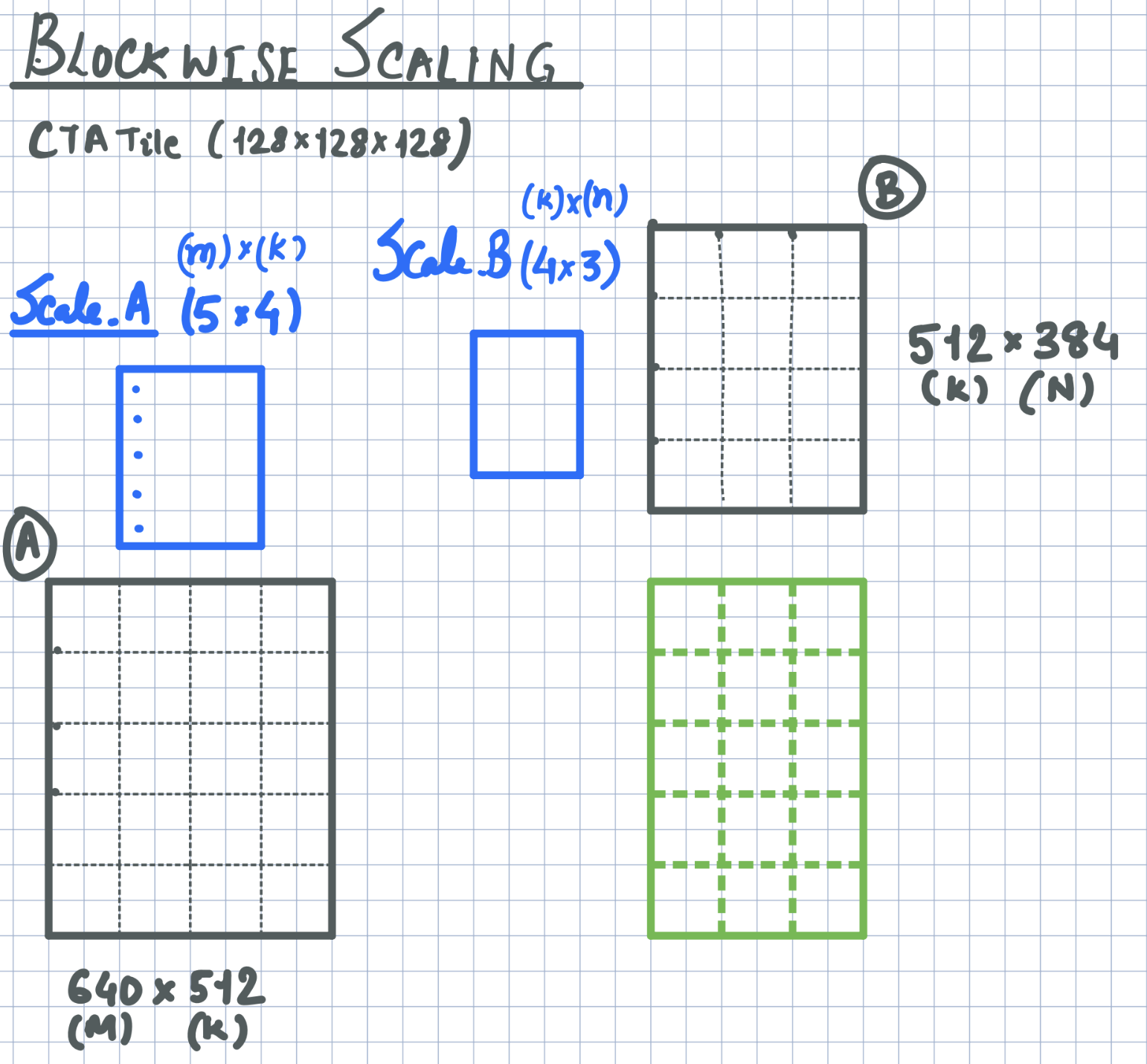
分块缩放实现

Cutlass分块缩放（Blockwise Scaling）实现

正如实现描述，下图展示了分块缩放的通用矩阵乘法（GEMM），操作数张量 A 和 B 以灰色显示，块缩放张量为蓝色，输出为绿色。在这个实现中，我们使用UTMALDG加载操作数张量，并使用LDGSTS加载块缩放张量，将它们从全局内存传输到共享内存。块缩放张量的加载与操作数张量的加载在同一阶段进行。为了确保LDGSTS的正确同步，我们使用带有noinc修饰符的cutlass::arch::cpasync_barrier_arrive。我们已经修改了PipelineTmaAsync类，以适应不同数量的生产者线程到达事件，从而有效地支持此功能。

分组缩放实现

Cutlass分组缩放（Groupwise Scaling）实现

由于#1932添加了分块缩放策略，此 PR 是基于#1932的补丁，并在 A 张量中沿 M 添加了分组缩放策略。沿 M 的缩放粒度与 CTA 块配置无关，但是，沿 N 和 K 的缩放粒度仍然是分块的（即每个 CTA 块一个缩放值）。 此 PR 将沿 M 的缩放粒度限制为 CTA 块配置中TILE_SHAPE_M的倍数，同时可以将 GEMM 沿 M 的缩放粒度精确设置为TILE_SHAPE_M（即回退到分块缩放策略），并在输入张量ScaleA上调用repeat_interleave方法来模拟缩放粒度是TILE_SHAPE_M的倍数的情况。

在这种实现中，我们将比“#1932”具有更多元素的缩放张量加载到共享内存中，因为每个 CTA 块可能沿 M 有各种不同的缩放。然而，由于每个线程的 WGMMA 累加器在结果张量中仅涉及两行，所以每个迭代中每个线程仅需要从共享内存将 A 张量的最多两个缩放值和 B 张量的恰好一个缩放值加载到寄存器中。

评论